A student wanted to determine if gummi bears tend to travel farther when they are placed on their back or on their belly prior to launching from a catapult.
The student collected data to address this problem and recorded the distance traveled in inches for 50 gummi bears in each group. The five number summaries for the two groups are shown below.
| Minimum | First Quartile | Median | Third Quartile | Maximum | |
| Back | 14 | 16 | 17.5 | 19 | 20 |
| Belly | 13 | 15 | 16.5 | 18 | 19 |
(a) Construct boxplots to summarize and compare the results.
(b) The difference between the two medians is 1 inch. Considering the amount of variability in the distance travelled, is this difference meaningful? Explain.
(c) Write a concluding statement regarding whether the placement of the gummi bear (back or belly) makes a difference?
Overview of the question
This question is designed to assess the student’s ability to:
1. Construct a box plot using the values in a five number summary (part (a)).
2. Informally assess the degree of overlap of two numerical data distributions with similar variability (parts (b) and (c)).
3. Use measures of center and variability to draw informal comparative inferences (parts (b) and (c)).
Standards
6.SP.4: Display numerical data in plots on a number line, including dot plots, histograms, and box plots.
7.SP.3: Informally assess the degree of visual overlap of two numerical data distributions with similar variabilities, measuring the difference between the centers by expressing it as a multiple of a measure of
variability.
7.SP.4: Use measures of center and measures of variability for numerical data from random samples to draw informal comparative inferences about two populations.
Ideal response and scoring
Part (a):
Part (a) asks students to construct boxplots from given five number summaries. The ideal response shows correctly drawn boxplots, labels the boxplots to indicate which represents the belly position and which represents the back position, and includes a scale that is labeled to indicate that the variable of interest is the distance traveled. If correct boxplots are provided, but the response is missing the scale and/or labels, the response is considered to be only partially correct for part (a). Responses that included graphs that were not boxplots, such as a comparative bar chart of the numbers in the five number summary or a scatterplot that is based on the numbers in the five number summary are considered to be incorrect for part (a).
Part (b):
Part (b) asks students to judge whether the difference between the two median of 1 inch is a meaningful difference considering the amount of variability in the distances traveled when the gummy bears were launched. This is the intent of the Grade 7 Common Core State Standards 7.SP.3 and 7.SP.4. An ideal response would note that the difference is not meaningful because 1 inch is small relative to the variability in the distances traveled (which is supported by an IQR of 3 inches and a Range of 6 inches).
Other acceptable explanations include noting that the distances traveled ranged from about 13 to 20 inches and that 1 inch is small relative to these distances or that there is a lot of overlap in the two boxplots constructed from the distance traveled data. Responses that indicated that the difference was not meaningful and that either provided a measure of variability or a reference to the magnitude of the distances traveled in the data sets but for which the explanation is incomplete or poorly communicated are considered to be partially correct for part (b).
Part (c):
Part (c) asks students to draw a conclusion based on data. After concluding that the difference between the two initial positions is not meaningful, an ideal response includes a clearly communicated statement that the position of the bear may not make a difference with a rationale that is based on the overlap in the boxplots or the answer given in part (b). A statement that indicates that the position of the bear may not make a difference but which is poorly communicated or for which the rationale is considered to be weak is scored as partially correct for part (c).
Sample responses indicating solid understanding
Part (a)
The following student response received a score of essentially correct for part (a). The box plots are correctly drawn and are labeled appropriately. A scale is provided and labeled to indicate that it represents distance.
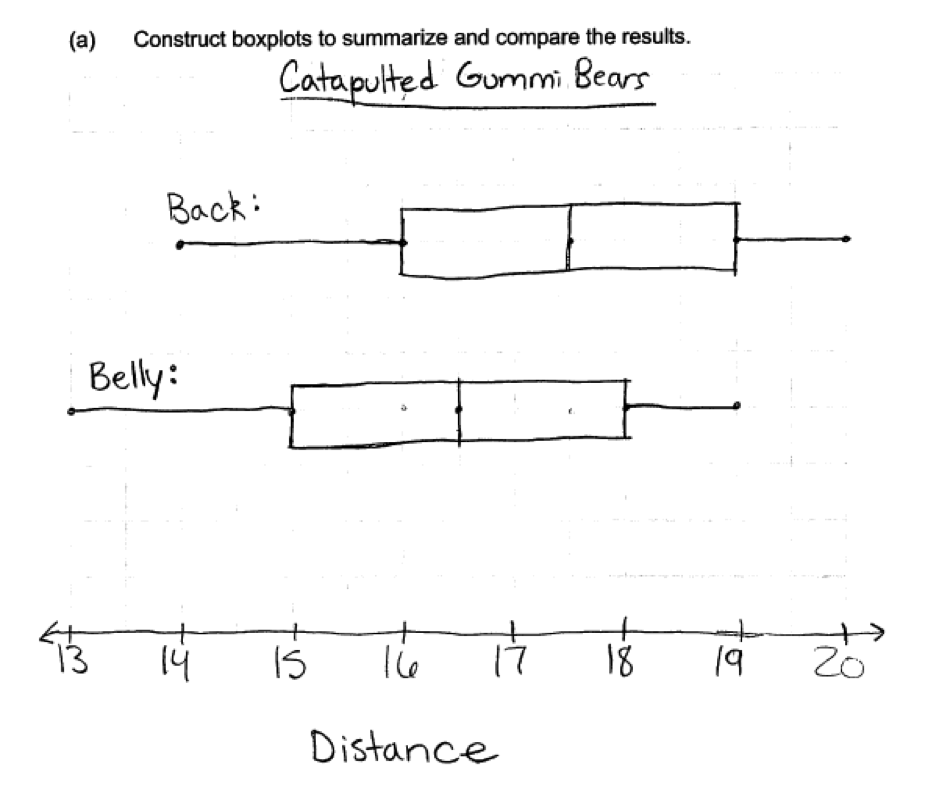 Parts (b) and (c). Students struggled with parts (b) and (c) and it was clear that the students participating in the pilot were unaware of the role that variability in the data plays in evaluating whether an observed difference is meaningful or not. The following student response demonstrates some understanding by comparing the difference of 1 inch to the magnitude of the medians (17.5), but the link to variability in the data or overlap in the two data distributions is missing. This response would have been stronger if it had made those connections.
Parts (b) and (c). Students struggled with parts (b) and (c) and it was clear that the students participating in the pilot were unaware of the role that variability in the data plays in evaluating whether an observed difference is meaningful or not. The following student response demonstrates some understanding by comparing the difference of 1 inch to the magnitude of the medians (17.5), but the link to variability in the data or overlap in the two data distributions is missing. This response would have been stronger if it had made those connections.

Common misunderstandings
Part (a) Construct a box plot using the values in a five number summary
Responses that were not scored as essentially correct for part (a) generally made one of two common mistakes. The most concerning of these mistakes is illustrated by the following three student responses. These responses indicate that the student does not know how to construct a box plot. The first two of these responses are typical of responses where the student created some form of bar graph or comparative bar graph using the numbers in the five number summary. In the third example below, the student has created a scatterplot using the values of the five number summaries plotted against the numbers 1,2,3,4 and 5. All three of these responses were scored as incorrect for part (a).
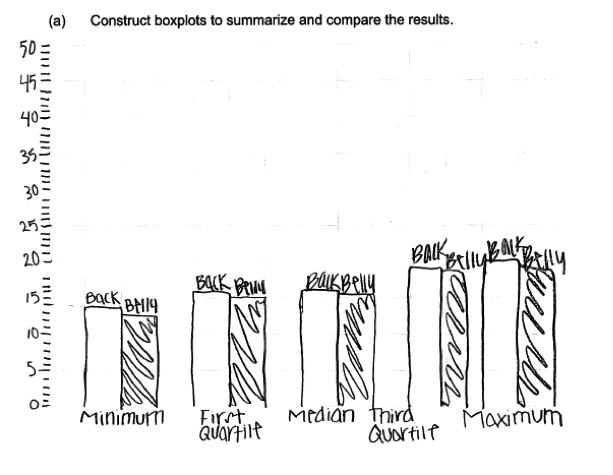
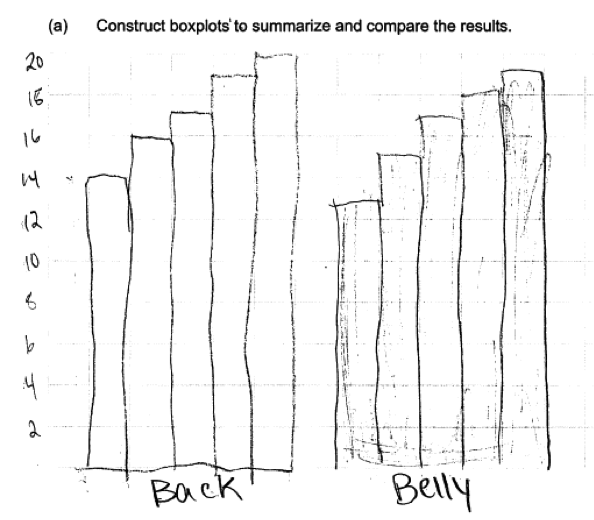
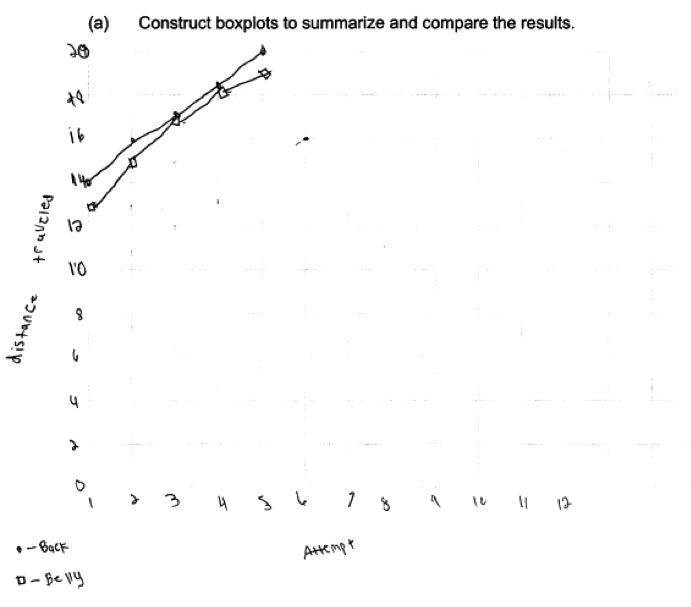 A second error that occurred in many student responses was the omission of labels and/or scales in the construction of the boxplots. For example, the following student response was scored as partially correct for part (a) because there is no scale indicated in the response.
A second error that occurred in many student responses was the omission of labels and/or scales in the construction of the boxplots. For example, the following student response was scored as partially correct for part (a) because there is no scale indicated in the response.
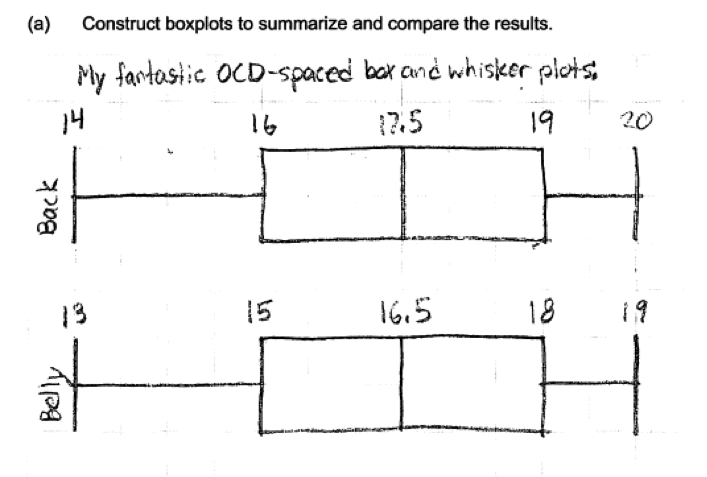 The following student response is typical of those that were scored as only partially correct for failure to include appropriate labels.
The following student response is typical of those that were scored as only partially correct for failure to include appropriate labels.
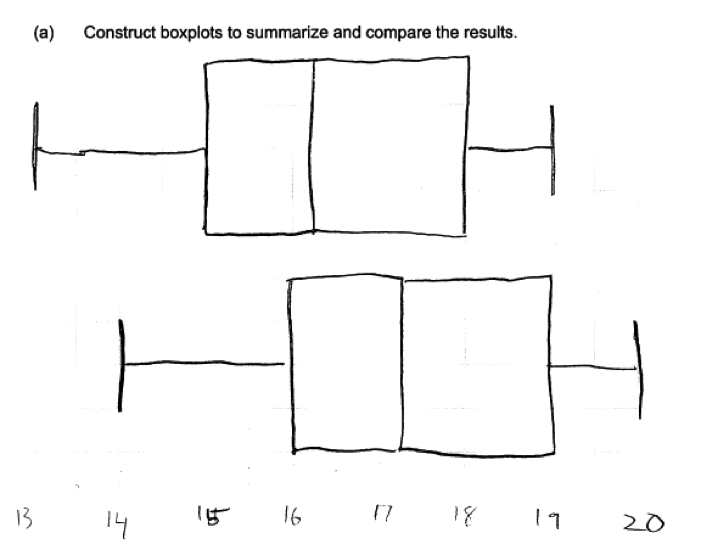
Parts (b) and (c)
Informally assess the degree of overlap of two numerical data distributions with similar variability
Use measures of center and variability to draw informal comparative inferences
Students found parts (b) and (c) difficult to answer and did not understand how to make informal inferences about the difference between two groups based on the overlap in the distributions. The two CCSS standards addressed in these two parts of this question are a challenge for both students and for teachers who have not previously had to develop this understanding.
One common error was to conclude that the difference of 1 inch was meaningful because every one of the statistics in the five number summery was exactly 1 inch smaller for the belly group. Students making this mistake did not recognize the need to decide if 1 inch was a large or small difference in medians relative to the variability in the data. The following three student responses illustrate this error.


 Some students concluded that the difference of 1 inch was not meaningful, but did not provide a justification based on variability in the data or overlap in the box plots. This is illustrated in the three student responses below.
Some students concluded that the difference of 1 inch was not meaningful, but did not provide a justification based on variability in the data or overlap in the box plots. This is illustrated in the three student responses below.


 Another student misconception is illustrated in the following student response. Because the difference in medians and quartiles are all 1, this student incorrectly concludes that a bear will always travel 1 inch farther if it is placed on its back.
Another student misconception is illustrated in the following student response. Because the difference in medians and quartiles are all 1, this student incorrectly concludes that a bear will always travel 1 inch farther if it is placed on its back.

Resources
More information about the topics assessed in this question can be found in the following resources.
Free Resources
Common Core Progressions Documents
A discussion on informal comparative inference and the intent of Common Core standards 7.SP.3 and 7.SP.4 and how this content might be developed in the classroom can be found in Common Core Tools progressions document for statistics in grades 6 – 8. See the discussion on pages 9 - 10.
Lessons
Statistics Education on the Web (STEW) has peer reviewed lessons plans. Some lessons related to the topic of this question are
Bubble Trouble. This lesson has students collect data and then use that data to
construct boxplots and draw informal conclusions. The content of this activity is
very similar to what students are asked to do when answering this LOCUS
question.
Tell It Like It Is! This lesson focuses on drawing and communicating conclusions
and is particularly relevant to part (c) of this LOCUS question.
Classroom and Assessment Tasks
Illustrative Mathematics has peer reviewed tasks that are indexed by Common Core Standard.
A task that involves drawing informal inferences about the differences between two groups is Offensive Linemen. Although this task uses dot plots rather than box plots in the comparison, the reasoning involved is similar to what is needed to answer parts (b) and (c) of this LOCUS question.
Guidelines for Assessment and Instruction in Statistics Education (GAISE)
Published by the American Statistical Association and available online, this document contains a discussion of using boxplots to compare distributions (pages 46 – 48).
Resources from the American Statistical Association
Bridging the Gap Between Common Core State Standards and Teaching Statistics is a collection of investigations suitable for classroom use. This book contains an investigation that involves using boxplots to make an informal inference and assessing the degree of visual overlap (How Fast Can You Sort Cards?, pages 126 – 140). The Example of ‘Interpret the Results’ section (pages 135 – 137) illustrates the type of reasoning needed to answer parts (b) and (c) of this LOCUS question.
Resources from the National Council of Teachers of Mathematics
The NCTM publication Developing Essential Understanding of Statistics in Grades 6 – 8 includes a section on comparing distributions on pages 42 – 51.The discussion of separation and overlap between distributions is particularly relevant to the content assessed in this LOCUS question.



