Note: This particular item has several instructional components and was developed only to be used on the pilot form of the LOCUS Assessments.
The scatterplots below show the number of wins plotted against the number of goals scored by a soccer team and the number of wins plotted against the number of goals allowed by a soccer team.
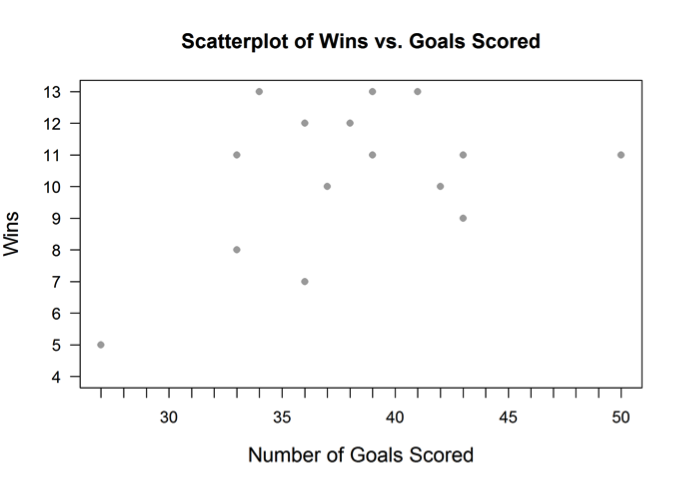

(a) Compare the associations displayed in the scatterplots. In which scatterplot does the association appear to be the stronger? Explain.
_______________________________________________________________________________________________________________________________________________________________________________________________________
This part of the question is intended for students that are unfamiliar with the QCR (quadrant count ratio). If you are familiar with the QCR, please proceed to the text just below this box.
One measure of the strength of an association is the QCR (quadrant count ratio). To calculate the QCR, divide the scatterplot into 4 quadrants by drawing a vertical line at the mean value for the explanatory variable (either Goals Scored or Goals Allowed), and by drawing a horizontal line a the mean value of the response variable (number of wins). Then, count the number of points in each quadrant and calculate:
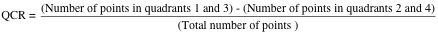
For example, here is the scatterplot for the number of wins plotted against the number of goals scored by a team, along with a vertical line at the mean number of goals scored (38.1) and a horizontal line at the mean number of wins (10.8).
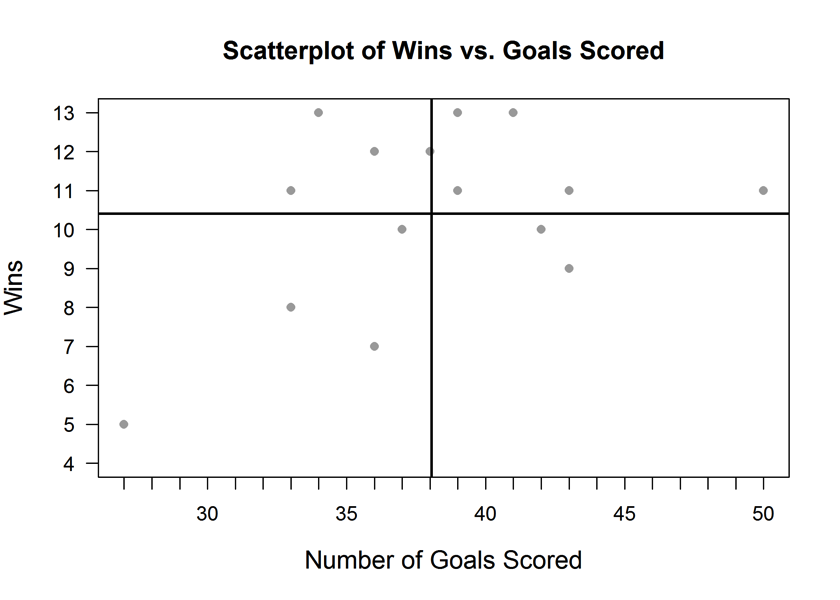 The QCR for the association between Wins and Goals Scored is:
The QCR for the association between Wins and Goals Scored is:
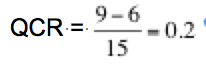
A QCR close to +1 suggests a strong positive association. A positive QCR close to 0 suggests a weak positive association. A QCR close to -1 suggests a strong negative association. A negative QCR close to 0 suggests a weak negative association.
Thus, a QCR of 0.2 is a positive number, and suggests a weak positive association between wins and goals scored.
_______________________________________________________________________________________________________________________________________________________________________________________________________
The scatterplot below shows the number of wins plotted against the number of goals allowed. The mean number of goals allowed is 38.1 and the mean number of wins is 10.4.
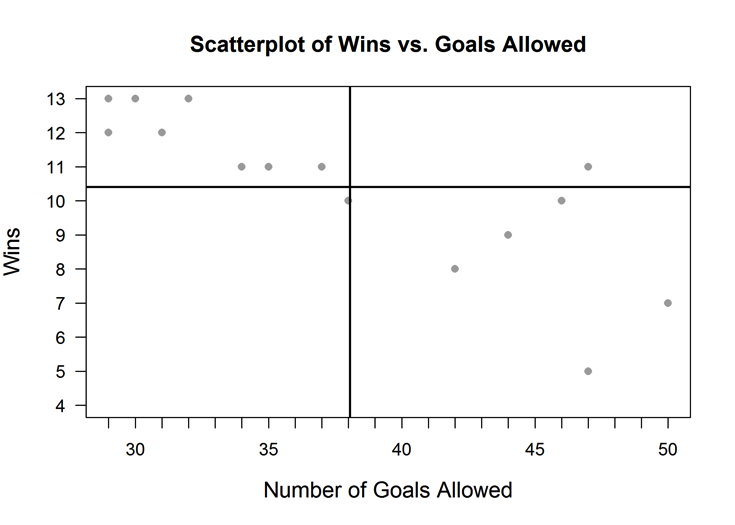 (b) Show that the QCR for the relationship between wins and goals allowed is -0.73.
(b) Show that the QCR for the relationship between wins and goals allowed is -0.73.
(c) The QCR between wins and goals scored is 0.2 and the QCR between wins and goals allowed is -0.73. Do these values confirm or contradict your response to part (a)? Explain.





 A correct response to part (a) could be worded in several different ways. This is illustrated by the following two student responses, which were also considered to be essentially correct for part (a).
A correct response to part (a) could be worded in several different ways. This is illustrated by the following two student responses, which were also considered to be essentially correct for part (a).
 The following student response indicates a good understanding of the content assessed in part (c). Although the explanation is not quite as complete as the one illustrated in the student response above, this response was also scored as essentially correct.
The following student response indicates a good understanding of the content assessed in part (c). Although the explanation is not quite as complete as the one illustrated in the student response above, this response was also scored as essentially correct.

 The following five student responses were all also scored as incorrect for part (a) because they indicate a lack of understanding of the concept of association.
The following five student responses were all also scored as incorrect for part (a) because they indicate a lack of understanding of the concept of association.



 Also in part (a), many students had difficult in describing the associations in the two scatterplots, resulting in what was considered a weak or incomplete explanation/justification for the choice of which scatterplot displayed the stronger association. The four student responses below are examples of responses that were scored as partially correct for part (a) for this reason.
Also in part (a), many students had difficult in describing the associations in the two scatterplots, resulting in what was considered a weak or incomplete explanation/justification for the choice of which scatterplot displayed the stronger association. The four student responses below are examples of responses that were scored as partially correct for part (a) for this reason.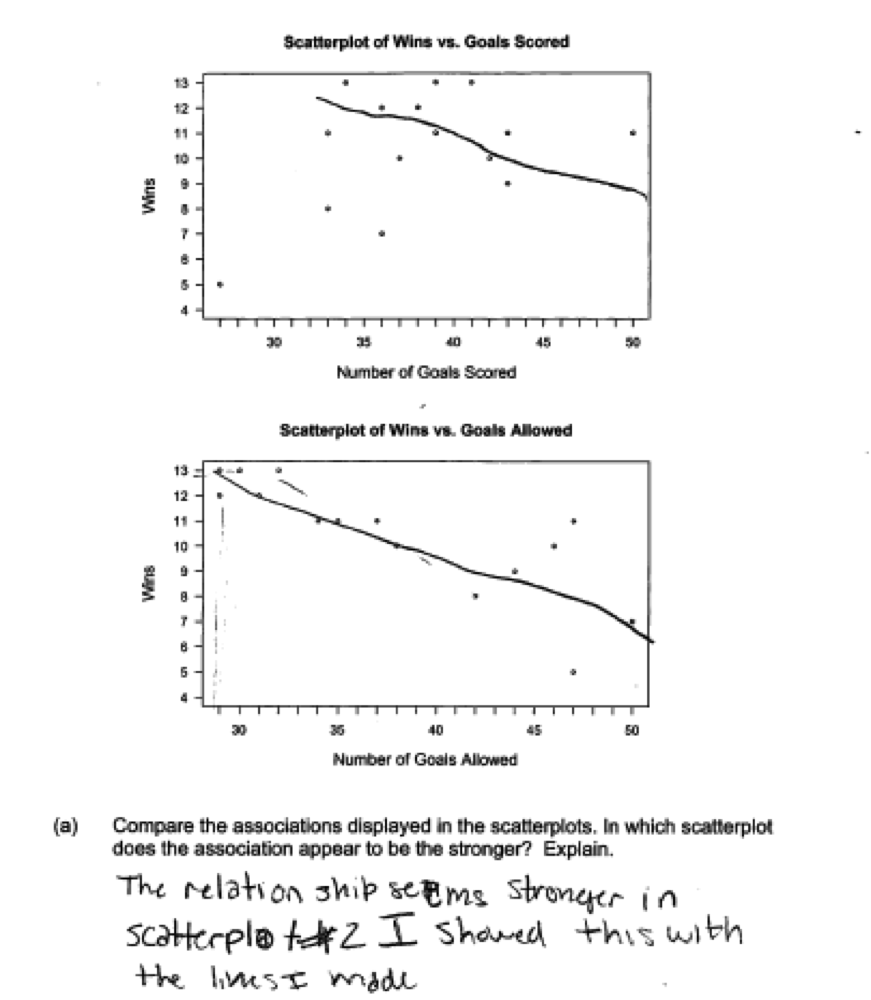



 Other students had difficulty calculating the QCR because they mislabeled the quadrants in the given scatterplot. This following student response is an example of this error.
Other students had difficulty calculating the QCR because they mislabeled the quadrants in the given scatterplot. This following student response is an example of this error.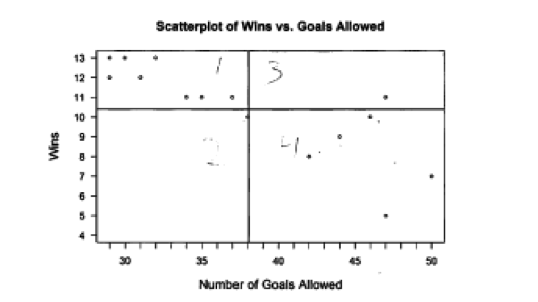 Other students used incorrect numbers in the calculation of the QCR. This is illustrated by the following two student responses. In the first response, the means for wins and goals allowed are used in the calculation rather than the quadrant counts. In the second response below, the quadrant counts from the example that used wins and goals scored are used rather than the quadrant counts for the given scatterplot for wins and goals allowed. Both of these responses were scored as incorrect for part (b).
Other students used incorrect numbers in the calculation of the QCR. This is illustrated by the following two student responses. In the first response, the means for wins and goals allowed are used in the calculation rather than the quadrant counts. In the second response below, the quadrant counts from the example that used wins and goals scored are used rather than the quadrant counts for the given scatterplot for wins and goals allowed. Both of these responses were scored as incorrect for part (b).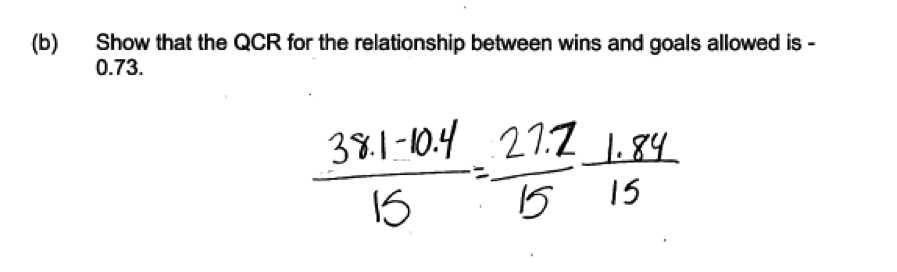

 The following student response is an example of the second common error in part (c), and illustrates a misinterpretation of the QCR. This response is considered incorrect for part (c).
The following student response is an example of the second common error in part (c), and illustrates a misinterpretation of the QCR. This response is considered incorrect for part (c).