A student wants to estimate the mean number of books that have been read by all students at his school over the summer. On Monday morning, he will survey the first 35 students who enter the library. Is this the best way to select a sample for this purpose?
(A) No. The student should survey students entering the library on more than one day of the week.
(B) No. The student should take a random sample of students entering the library instead.
(C) No. The student should take a random sample of students from all students, not just those entering the library.
(D) Yes. Selecting a sample in this way will not introduce the possibility of bias.




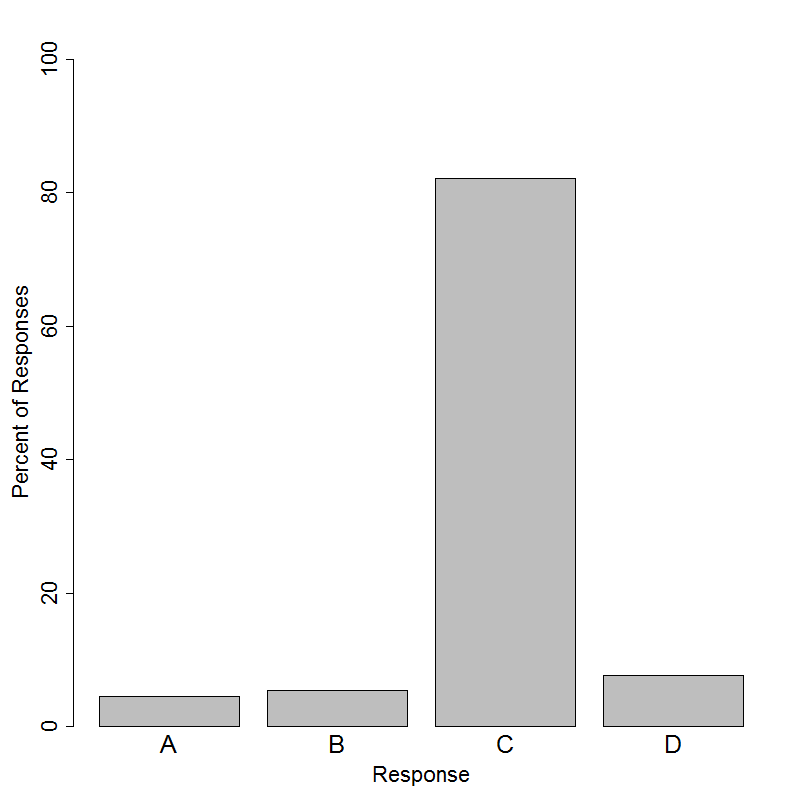
In order to estimate the mean number of books that have been read by all students at the school over the summer, a student decides to survey the first 35 students who enter the library. This sampling method is known as convenience sampling and will introduce bias in the survey results because the first 35 students are not randomly selected from the population of interest. To make generalizations about a population using a sample from that population, the sample must be representative of that population, and random sampling tends to produce more representative samples than convenience sampling. On the other hand, students entering the library on a Monday morning may not be representative of the larger student body since those students may be more avid readers. Surveying only those students could lead to conclusions that that might overestimate the mean number of books read by students at the school. Therefore, option (C) is the best answer, since it proposes taking a random sample from all students, not just those entering the library.
Surveying students entering the library on more than one day of the week, as suggested in option (A), does give more students the chance of being selected; however, in order for the sample to be representative of the population, all of the students must have an equal chance of being selected. Thus, Option (A) is incorrect as is Option (B). Option (B) introduces a random element, but it still excludes the students that might not enter the library. Option (D) is also not the correct answer for the reason discussed earlier about convenience sampling.