The city of Gainesville hosted two races last year on New Year’s Day. Individual runners chose to run either a 5K (3.1 miles) or a half-marathon (13.1 miles). One hundred thirty four people ran in the 5K, and 224 people ran the half-marathon. The mile time, which is the average amount of time it takes a runner to run a mile, was calculated for each runner by dividing the time it took the runner to finish the race by the length of the race. The histograms below show the distributions of mile times (in minutes per mile) for the runners in the two races.
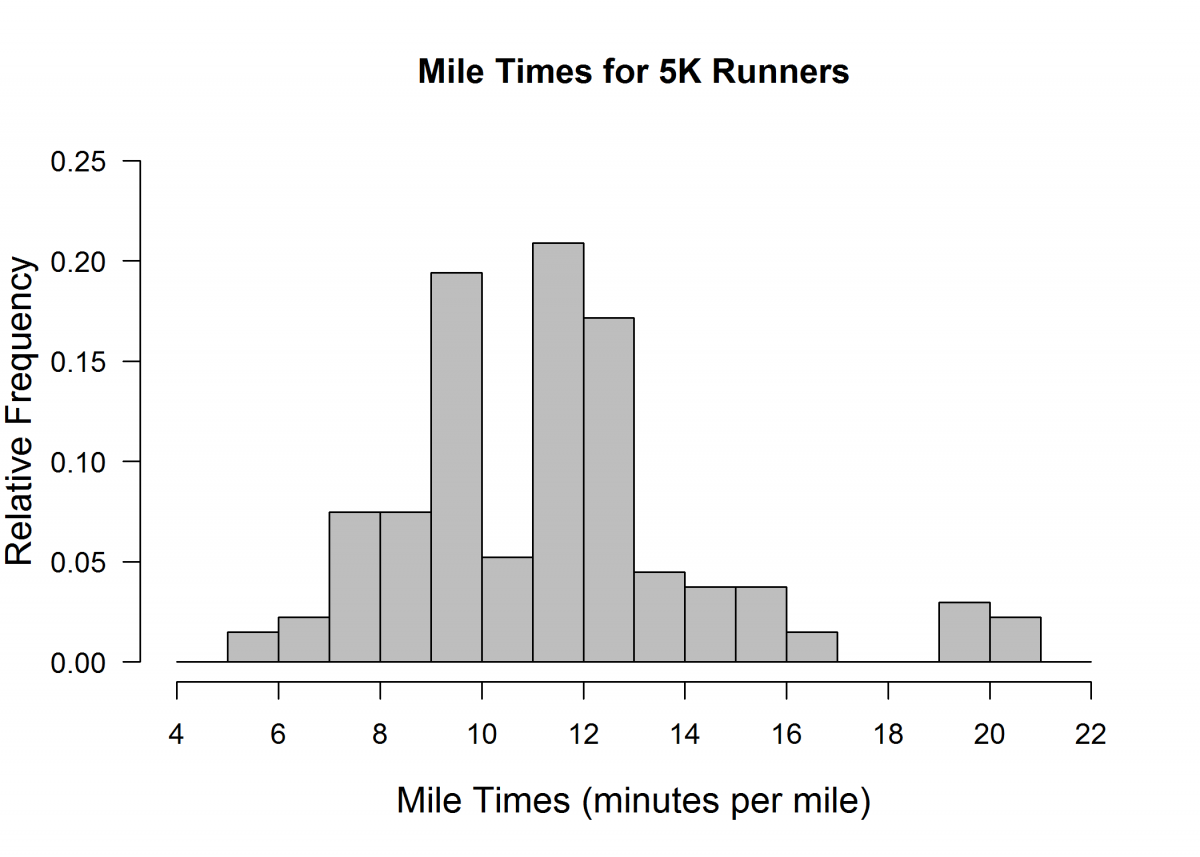
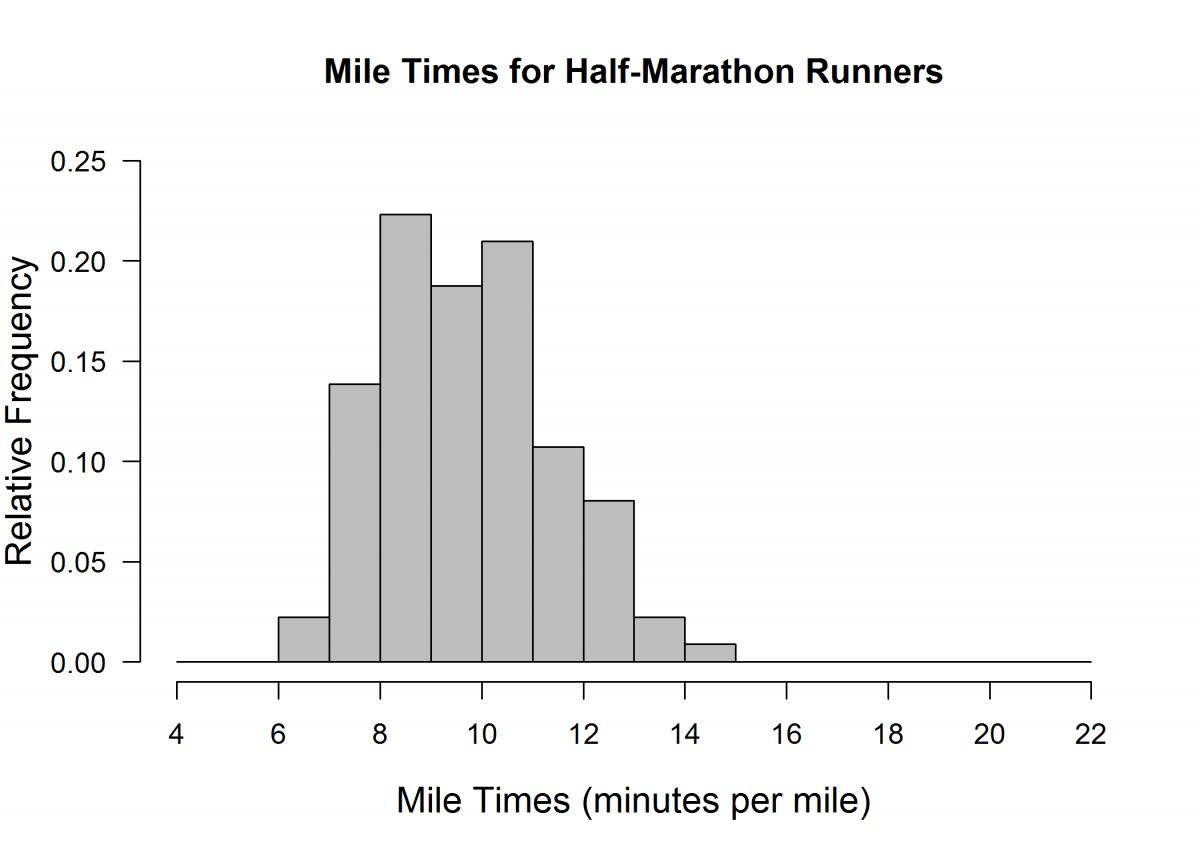
(a) Jaron predicted that the mile times of runners in the 5K race would be more consistent than the mile times of runners in the half-marathon. Do these data support Jaron’s statement? Explain why or why not.
(b) Sierra predicted that, on average, the mile time for runners of the half-marathon would be greater than the mile time for runners of the 5K race. Do these data support Sierra’s statement? Explain why or why not.
(c) Recall that individual runners chose to run only one of the two races. Based on these data, is it reasonable to conclude that the mile time of a person would be less when that person runs a half-marathon than when he or she runs a 5K? Explain why or why not.
Overview of the question
This question is designed to assess the student’s ability to:
1. Identify which of two distributions has the least variability (part(a)).
2. Identify which of two distributions has the greatest mean (part (b)).
3. Recognize questions that cannot be answered by the given data (part (c)).
Standards
6.SP.2: Understand that a set of data collected to answer a statistical question has a distribution which can be described by its center, spread, and overall shape.
6.SP.5: Summarize numerical data sets in relation to their context, such as by:
a. Reporting the number of observations.
b. Describing the nature of the attribute under investigation, including how it was measured and its units of measurement.
c. Giving quantitative measures of center (median and/or mean) and variability (interquartile range and/or mean absolute deviation), as well as describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered.
d. Relating the choice of measures of center and variability to the shape of the data distribution and the context in which the data were gathered.
7.SP.4: Use measures of center and measures of variability for numerical data from random samples to draw informal comparative inferences about two populations.
S-ID.3: Interpret differences in shape, center, and spread in the context of the data sets, accounting for possible effects of extreme data points (outliers).
Ideal response and scoring
Part (a):
Part (a) asks students to recognize that “more consistent” miles times means that there will be less variability and then to determine which of the two given histograms shows less variability in mile times. An ideal response to part (a) is one that recognizes that there is more variability in the mile times for the 5K race than for the half-marathon and indicates that Jaron’s prediction that the mile times of runners in the 5K race would be more consistent than the times for runners in the half-marathon is not correct.
Responses that correctly indicate that Jaron’s prediction is incorrect but which do not support the conclusion by comparing variability in the two distributions are considered to be partially correct for part (a). Also considered to be only partially correct are responses that correctly compare the variability in the two distributions but do not clearly indicate that Jaron’s prediction is not supported. Responses that indicate that Jaron’s statement is supported are considered incorrect for part (a).
Part (b):
An ideal response to part (b) is one that recognizes that the mean mile time is greater for the mile times for the 5K race than for the half-marathon and indicates that Sierra’s prediction that the mile time, on average, of runners in the half-marathon would be greater than the time, on average, for runners in the 5K race is not correct.
Responses that correctly indicate that Sierra’s prediction is incorrect but which do not support the conclusion by comparing the centers of the two distributions are considered to be partially correct for part (b). Also considered partially correct for part (b) are responses that say that Sierra’s prediction is supported and base that conclusion on the fact that the difference in where the two distributions are centered is not very large. Responses that indicate that Sierra’s prediction is not supported but which do not provide an explanation are considered incorrect for part (b).
Part (c):
In part (c), students are asked if it is reasonable to conclude that the mile time would be less if a person ran a half-marathon than if that person ran a 5K race. An ideal response indicates that it is not reasonable and provides an explanation that is based on the fact that the runners in these races chose the race in which they would run.
Responses that indicate that the stated conclusion is not reasonable but that do not explicitly mention choice of race in the explanation are considered partially correct for part (c). Responses with explanations that are not based on the study design (the way in which the data were collected) are considered incorrect for part (c).
Sample responses indicating solid understanding
The following student response illustrates ideal responses to parts (a) and (b) of this question. The student does a good job of explaining why Jaron’s prediction is not supported based on variability in the distributions and why Sierra’s prediction is not supported based on a comparison of the centers of the distribution. Both parts (a) and (b) of this student response were scored as essentially correct.

The following student response shows a good understanding of the concepts assessed by this question. In part (a) the response indicates that Jaron’s prediction is not supported and justifies this in terms of “more spread” in the mile times for the 5K runners. In part (b), the response correctly indicates that the average for the 5K race mile times is greater than the average for the mile times for the half-marathon race. The response to part (c) states that the given conclusion is not valid and justifies this based on the fact that runners got to pick which race they would run. All three parts of this response were scored as essentially correct and this student response received a score of 4.

The following student response also demonstrates solid understanding of the concepts assessed in this question. Because raw data is not provided, it is not possible to actually calculate the ranges or mean for the two given distributions, so the reported values given in this student response are just approximations of these values based on the histograms. This was considered to be a minor error in communication that was not penalized in the scoring, and this student response also received a score of 4 for this question.

Common misunderstandings
A common error that appeared on all parts of this question was made by students who confused the mile time with the time to run the entire marathon. Students who made this mistake often answered the questions posed based the fact that one race was longer than the other and did not base their answers on the given distributions. Such responses were scored as incorrect. This error is illustrated by the following student response to parts (b) and (c) shown below.

Part (a): Identify which of two distributions has the least variability.
Many students struggled with part (a) of this questions, and we saw a number of different errors in the responses to this question. The most concerning of these errors is illustrated in the three student responses below. In each of these responses, the student has confused variability in the heights of the bars in the histogram (frequencies) with variability in the data (mile times). This represents a clear misunderstanding of how a histogram serves as a graphical summary of a data distribution. Each of these responses was scored incorrect for part (a).



Other common errors in part (a) responses are illustrated in the following student responses. The response below is typical of those from students who believed that “more consistent” means more variability rather than less variability in the mile times. Students who made this error indicated that the data supported Jaron’s prediction, and were scored as incorrect for part (a).

Other students interpreted the existence of outliers as an indication of inconsistency. While the presence of outliers is a factor in assessing variability, the following student response provides a justification that is based only on the presence or absence of outliers. Because this explanation is not clearly tied to variability in the two distributions, this response was scored as only partially correct for part (a).

Other students provided explanations that were not based on variability in the distributions. This is illustrated in the following two student responses, both of which were scored as incorrect for part (a).


In addition to the errors mentioned above, there were some students who did not base their response on the given data on mile times for the two races. The student response below, which was scored as incorrect for part (a), is typical of students making this error.

Part (b): Identify which of two distributions has the greatest mean.
There were three common student errors in student responses to part (b). The most common error is illustrated by the two student responses that follow. In each case, the student did not recognize that answering this questions requires a comparison of where the two distributions are centered.


A second common error in answering part (b) is illustrated in the following student response. While this student is on the right track, this response was considered to be only partially correct because there is no clear comparison of the distribution centers.

The third common student error is a bit puzzling and was made by students who provided a correct comparison of the distribution centers, but then reached an incorrect conclusion about Sierra’s prediction. It is possible that these students were just careless in writing their answers, but because the stated conclusion in these responses is incorrect, they were scored as only partially correct.


Part (c): Recognize questions that cannot be answered by the given data.
Many students struggled with part (c) of this question. Some students reached an incorrect conclusion while others indicated that the stated conclusion was not reasonable but did not provide an explanation that was related to the study design and the fact that runners chose which race they would run.
For example, consider the following four student responses. While these responses correctly state that the conclusion is not reasonable, they were scored as incorrect for part (c) because the explanation provided is not based on the given data or study design.
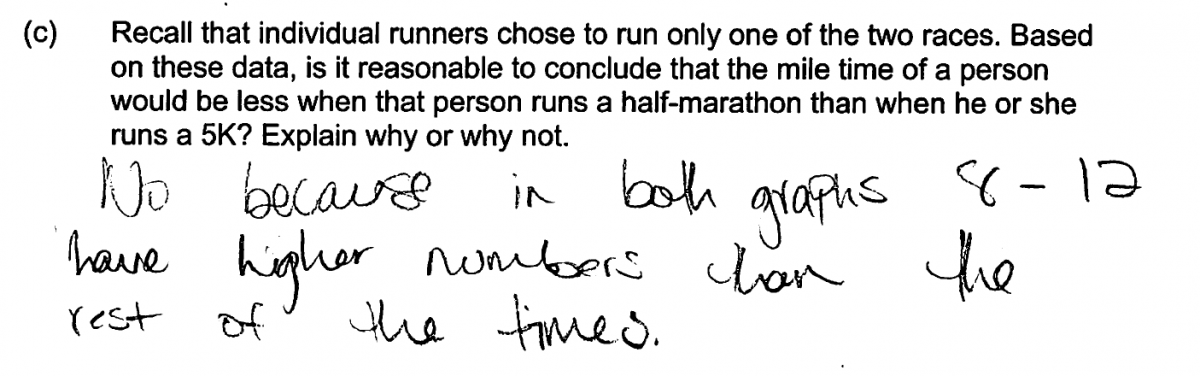



The following three student responses illustrate the other common error in answering part (c). In each of these responses, the student indicates that the stated conclusion is reasonable, which is not correct based on the way the data were collected.



Resources
Resources
More information about the topics assessed in this question can be found in the following resources.
Free Resources
Guidelines for Assessment and Instruction in Statistics Education (GAISE)
Published by the American statistical Association and available online, this document contains a section on representing data distributions on pages 44 – 46.
Classroom and Assessment Tasks
Illustrative Mathematics has peer reviewed tasks that are indexed by Common Core Standard. Two tasks relevant to the content of this Locus question are:
Is it Center or is it Variability?
Resources from the National Council of Teachers of Mathematics
The NCTM publication Developing Essential Understanding of Statistics in Grades 6 – 8 includes a section on comparing distributions (pages 42-46) that is particularly relevant to the concepts assessed in this Locus question.



