A survey of 400 adults in a certain city was conducted. Data on gender and support for a particular candidate are summarized in the two-way table below.
| Male | Female | Total | |
| Support | 112 | 102 | 214 |
| Do Not Support | 70 | 116 | 186 |
| Total | 182 | 218 | 400 |
What proportion of those who responded "Support" are male?
(A) 112/400
(B) 182/400
(C) 112/214
(D) 112/182
Standards
8.SP.4: Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table. Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects. Use relative frequencies calculated for rows or columns to describe possible association between the two variables. For example, collect data from students in your class on whether or not they have a curfew on school nights and whether or not they have assigned chores at home. Is there evidence that those who have a curfew also tend to have chores?
S-ID.5: Summarize categorical data for two categories in two-way frequency tables. Interpret relative frequencies in the context of the data (including joint, marginal, and conditional relative frequencies). Recognize possible associations and trends in the data.
Correct answer and commentary
Student performance
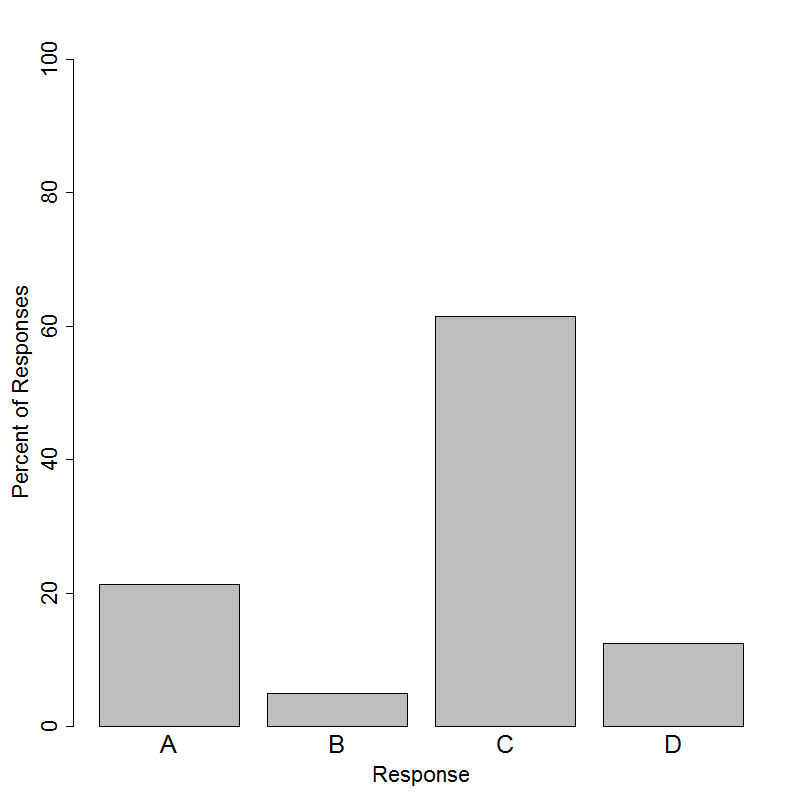
The correct answer to this question is Option (C). The question requires students to calculate a conditional relative frequency. The term relative frequency refers to the use of proportions or percents (instead of counts) to describe how many individuals fall into a particular category. When we calculate the proportion of individuals that fall into a category within a particular group, it is called a conditional relative frequency. Since we are interested in the distribution of gender among those who support the candidate, we can imagine covering the rest of rest of the table and restricting our attention to the Support row. Within this group of 214 supporters, 112 are male, so the correct answer is 112/214.
None of the other answer options appropriately calculate the proportion of the candidate’s supporters who are male. The most popular incorrect answer option was (A), the proportion of the full sample who are both male and supporters of the candidate. Option (B) is the proportion of the full sample who are male. This proportion can be used to describe the distribution of gender in the total sample, but it does not tell us anything about the relationship between gender and support for the candidate. Option (D) is the proportion of males who support the candidate. This describes the candidate’s support among a particular gender instead of the distribution of gender among the candidate’s supporters.