A random sample of 411 high school students was selected in order to compare the heights, in centimeters (cm), of vegetarians and nonvegetarians. The relative-frequency histograms below show the distributions of height for the 15 students who said that they were vegetarian and for 396 students who said they were not vegetarian.
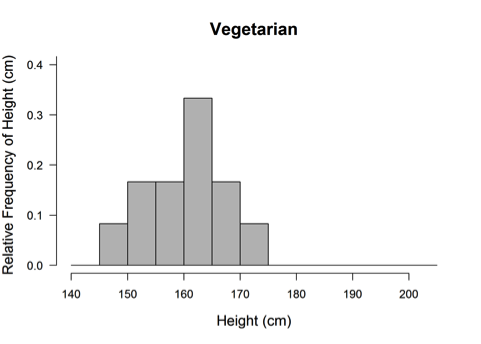
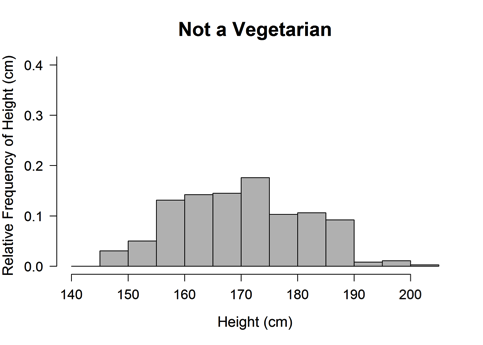 (a) Write a few sentences comparing the distributions of height for the vegetarians and nonvegetarians.
(a) Write a few sentences comparing the distributions of height for the vegetarians and nonvegetarians.
(b) Explain why it is better to use relative frequencies (proportions) rather than frequencies (counts) when comparing the vegetarians and nonvegetarians.
(c) Based on the design of this study, would it be reasonable to conclude that being a vegetarian causes students to be shorter, on average? Explain.
Overview of the question
This question is designed to assess the student’s ability to:
1. Compare two groups based on graphical display of the two data distributions (part (a)).
2. Explain why relative frequencies should be used when comparing groups that have different sample sizes (part (b)).
3. Explain why it is not reasonable to draw a cause-and-effect conclusion in the context of an observational study (part (c)).
Standards
6.SP.2: Understand that a set of data collected to answer a statistical question has a distribution which can be described by its center, spread, and overall shape.
6.SP.5: Summarize numerical data sets in relation to their context, such as by: a) Reporting the number of observations; b) Describing the nature of the attribute under investigation, including how it was measured and its units of measurement; c) Giving quantitative measures of center (median and/or mean) and variability (interquartile range and/or mean absolute deviation), as well as describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered; d) Relating the choice of measures of center and variability to the shape of the data distribution and the context in which the data were gathered.
7.SP.4: Use measures of center and measures of variability for numerical data from random samples to draw informal comparative inferences about two populations.
S-ID.2: Use statistics appropriate to the shape of the data distribution to compare center (median, mean) and spread (interquartile range, standard deviation) of two or more di"erent data sets.
S-IC.1: Understand statistics as a process for making inferences about population parameters based on a random sample from that population.
S-IC.3: Recognize the purposes of and di"erences among sample surveys, experiments, and observational studies; explain how randomization relates to each.
S-IC.6: Evaluate reports based on data.
Ideal response and scoring
Part (a):
Part (a) asks students to compare two data distributions that have been displayed using histograms. An ideal response to part (a) is one that provides a comparison of (1) center, (2) spread, and (3) shape and which uses comparative language (smaller, larger, greater, lesser, etc.) in at least one of these three comparisons.
Responses that compare the distributions on only one or two of the three characteristics (center, spread and shape) are considered to be partially correct. Responses that describe center, spread and shape for each of the two distributions, but which fail to actually compare the two distributions are also considered partially correct.
Part (b):
An ideal response to part (b) recognizes that the numbers of observations used to construct the histograms are quite different for the two groups (15 for vegetarians and 396 for nonvegetarians) and notes that as a result of the different group sizes, comparisons of based on frequencies rather than relative frequencies would not be meaningful and could be misleading.
A response that says comparisons are easier to make using relative frequencies or that comparisons are more meaningful when relative frequencies are used but does not specifically mention the difference in groups sizes is considered partially correct.
Part (c):
Part (c) asks if it is reasonable to conclude that being vegetarian causes students to be shorter, on average. An ideal response to part (c) is one that recognizes that the study described is an observational study and that it is not reasonable to draw cause-and-effect conclusions from an observational study. Responses might also say that the study was not an experiment, or that there was no random assignment to treatments, or provides a good explanation linked to a possible confounding variable. Such responses are also considered essentially correct, even if the term “observational study” is not used.
Responses that correctly say that a cause-and-effect conclusion is not reasonable but give a weak or incomplete explanation (such as “association is not causation” or “there may be confounding”) are considered to be partially correct. Any response that contains an incorrect explanation (such as “you need larger samples”) or that concludes that the cause-and-effect conclusion is reasonable is considered incorrect.
Sample responses indicating solid understanding
The following student response shows a good understanding of the concepts assessed by this question and received a score of 4. In part (a) the two distributions are described in terms of center, spread and shape, and comparative language is used (“greater center”, “less variable”). Although numerical values for center are given in the response, this is not required and this response to part (a) would still have been scored as essentially correct even if they had not been included.
 The response in part (b) acknowledges the unequal group sizes and gives a nice explanation of why relative frequencies should be used in comparisons.
The response in part (b) acknowledges the unequal group sizes and gives a nice explanation of why relative frequencies should be used in comparisons.
 The response in part (c) correctly indicates that it is not reasonable to draw a cause-and-effect conclusions and appeals to the fact that the study described was an observational study. With all three parts scored as essentially correct, this student response received a score of 4.
The response in part (c) correctly indicates that it is not reasonable to draw a cause-and-effect conclusions and appeals to the fact that the study described was an observational study. With all three parts scored as essentially correct, this student response received a score of 4.
 In part (a) ideally the response would make an actual comparison of center, spread and shape, but to receive a score of essentially correct on part (a), the rubric requires only at least one comparison. The student response to part (a) shown below was scored as essentially correct even though it only makes one comparative statement (for spread, in terms of “larger range”) because it still does address all three characteristics of center, spread and shape.
In part (a) ideally the response would make an actual comparison of center, spread and shape, but to receive a score of essentially correct on part (a), the rubric requires only at least one comparison. The student response to part (a) shown below was scored as essentially correct even though it only makes one comparative statement (for spread, in terms of “larger range”) because it still does address all three characteristics of center, spread and shape.
 Below is a second example of a response to part (b) that was scored as essentially correct. The response clearly refers to the different group sizes in the explanation of why relative frequencies should be used.
Below is a second example of a response to part (b) that was scored as essentially correct. The response clearly refers to the different group sizes in the explanation of why relative frequencies should be used.
 Typically, responses to part (c) that were scored as essentially correct appealed to the fact that the study was an observational study, but there were other ways of wording the response that could still receive a score of essentially correct for part (c). In the following response to part (c), the response would have been scored as only partially correct had the student stopped after the first sentence because the explanation would have been considered weak and incomplete. But the response goes on to indicate that the study was not an experiment and that there might be extraneous variables, resulting in a score of essentially correct. The statement that “This information gathered from the study is not representative of the entire population” was considered to be extraneous and was overlooked.
Typically, responses to part (c) that were scored as essentially correct appealed to the fact that the study was an observational study, but there were other ways of wording the response that could still receive a score of essentially correct for part (c). In the following response to part (c), the response would have been scored as only partially correct had the student stopped after the first sentence because the explanation would have been considered weak and incomplete. But the response goes on to indicate that the study was not an experiment and that there might be extraneous variables, resulting in a score of essentially correct. The statement that “This information gathered from the study is not representative of the entire population” was considered to be extraneous and was overlooked.
 Three other sample responses that were scored as essentially correct for part (c) are shown below. The first two responses appeal to the fact that the study was not an experiment, without mentioning the term observational study. The third gives an example of a plausible potential confounding variable (gender).
Three other sample responses that were scored as essentially correct for part (c) are shown below. The first two responses appeal to the fact that the study was not an experiment, without mentioning the term observational study. The third gives an example of a plausible potential confounding variable (gender).



Common misunderstandings
Part (a) asked students to compare two groups based on graphical displays of the two data distributions. Responses that were not considered essentially correct on part (a) generally made one of two errors. Some described center, spread and shape for each distribution, but failed to actually compare the two distributions. This error is illustrated in the following student response which was scored as only partially correct for part (a).

The other common student error on part (a) was failure to address all three characteristics of center, spread and shape. For example, the following two student responses were scored as only partially correct because although they address variability and make at least one comparative statement, neither address center.

 The three sample responses below also fail to address one or more of the three characteristics and all were scored as only partially correct for part (a).
The three sample responses below also fail to address one or more of the three characteristics and all were scored as only partially correct for part (a).


 Part (b) asked students to explain why relative frequencies should be used when comparing groups that have different sample sizes. The two common errors in part (b) were either failure to specifically mention the difference in group sizes or providing incorrect explanations. For example, the response below was scored as partially correct because the explanation was not tied to group sizes.
Part (b) asked students to explain why relative frequencies should be used when comparing groups that have different sample sizes. The two common errors in part (b) were either failure to specifically mention the difference in group sizes or providing incorrect explanations. For example, the response below was scored as partially correct because the explanation was not tied to group sizes.
 The following student responses illustrate incorrect explanations for the need to use relative frequencies. All of these responses were scored as incorrect for part (b).
The following student responses illustrate incorrect explanations for the need to use relative frequencies. All of these responses were scored as incorrect for part (b).




Part (c) asked students to explain why it is not reasonable to draw a cause-and-effect conclusion in the context of an observational study. Many students struggled with part (c), often providing incorrect explanations or reaching an incorrect conclusion. Some reached a correct conclusion, but provided a weak or incomplete explanation.
The following two responses were scored as only partially correct for part (c) because the explanations were viewed as weak or incomplete. Both refer to confounding/extraneous variables, but neither give a plausible example of such a variable in the context of the given problem.

 Some students gave an incorrect explanation that was based on the belief that you could only draw a cause-and-effect conclusion if the two group sizes were equal, as illustrated in the following student responses, which were scored as incorrect for part (c).
Some students gave an incorrect explanation that was based on the belief that you could only draw a cause-and-effect conclusion if the two group sizes were equal, as illustrated in the following student responses, which were scored as incorrect for part (c).

 Others expressed the belief that a cause-and-effect conclusion was not justified because the sample size was too small. This is illustrated in the following response, which was scored as incorrect for part (c).
Others expressed the belief that a cause-and-effect conclusion was not justified because the sample size was too small. This is illustrated in the following response, which was scored as incorrect for part (c).
 The following student responses were also scored as incorrect for part (c) and illustrate other incorrect beliefs about the conditions under which a cause-and-effect conclusion is reasonable.
The following student responses were also scored as incorrect for part (c) and illustrate other incorrect beliefs about the conditions under which a cause-and-effect conclusion is reasonable.

 Finally, some students reached an incorrect conclusion, thinking that it is possible to draw a cause –and-effect conclusion based on the observational study described. The following two responses illustrate this type of error, and were scored as incorrect for part (c).
Finally, some students reached an incorrect conclusion, thinking that it is possible to draw a cause –and-effect conclusion based on the observational study described. The following two responses illustrate this type of error, and were scored as incorrect for part (c).


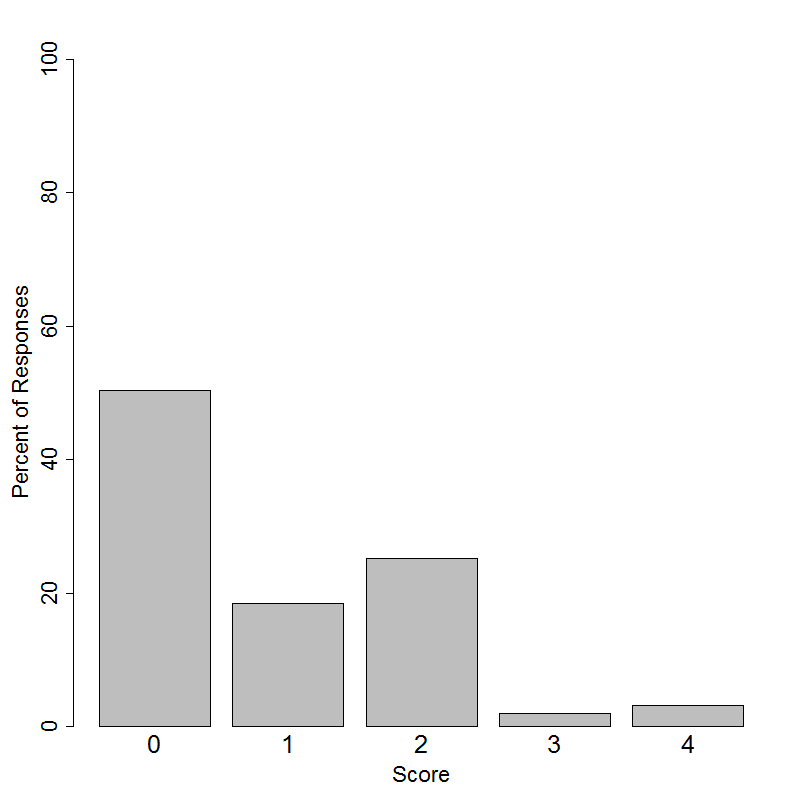
Student performance
Resources
Free Resources
Classroom and Assessment Tasks
Illustrative Mathematics has peer reviewed tasks that are indexed by Common Core Standard. A task that focuses on the role of study design in the type of conclusion that can be drawn and could be the basis of a productive classroom discussion is
High Blood Pressure
https://www.illustrativemathematics.org/content-standards/HSS/IC/B/3/tas...
Resources from the American Statistical Association
Bridging the Gap Between Common Core State Standards and Teaching Statistics is a collection of investigations suitable for classroom use. This book contains a section on describing distributions (Section 3) and a section on comparing groups (Section 4). The activities in these two sections develop the skills assessed in part (a) of this question. For more information see
http://www.amstat.org/education/btg/index.cfm
Resources from the National Council of Teachers of Mathematics
The NCTM publication Developing Essential Understanding of Statistics in Grades 6 – 8 includes a section on comparing distributions on pages 42 – 51.For information see
http://www.nctm.org/catalog/product.aspx?ID=13800
The NCTM publication Developing Essential Understanding of Statistics in Grades 9 –12 includes a discussion of the following essential understanding: Random selection and random assignment are different things, and the type and scope of conclusions that can be drawn from data depend on the role of random selection and random assignment in the study design (see pages 65 – 66). This discussion is relevant to the content assessed in part (c) of this question. For information see
http://www.nctm.org/catalog/product.aspx?ID=14617
The NCTM publication Navigating through Data Analysis in Grades 9 – 12 includes a chapter on designing studies and explores the types of conclusions that are reasonable for different types of studies (see Chapter 4 titled “Designing Studies”). For more information see
http://www.nctm.org/catalog/product.aspx?id=12326



