A department store manager wants to know which of two advertisements is more effective in increasing sales among people who have a credit card with the store. A sample of 100 people will be selected from the 5,300 people who have a credit card with the store. Each person in the sample will be called and read one of the two advertisements. It will then be determined if the credit card holder makes a purchase at the department store within two weeks of receiving the call.
(a) Describe the method you would use to determine which credit card holders should be included in the sample. Provide enough detail so that someone else would be able to carry out your method.
(b) For each person in the sample, the department store manager will flip a coin. If it lands heads up, advertisement A will be read. If it lands tails up, advertisement B will be read. Why would the manager use this method to decide which advertisement is read to each person?
Overview of the question
This question is designed to assess the student’s ability to:
1. Recognize the need for random selection and describe a method for selecting a random sample from a given population (part (a)).
2. Explain why random assignment to treatments is important in the design of a statistical experiment (part (b)).
Ideal response and scoring
Part (a):
An ideal response to part (a) uses random selection in a planned way to determine which of the store’s 5300 credit card holders will be included in the sample. To be considered essentially correct for part (a) the response must indicate how the random selection will be implemented. A response that indicates the need for random selection, but which does not provide an adequate description of how the random selection will be accomplished (for example, a response that just says pick 100 people at random from the list) is considered partially correct.
Part (b):
An ideal response to part (b) provides an explanation that indicates that the random assignment to treatments in the experiment described allows the store manager to conclude that which advertisement is read is the cause of any observed difference in the proportion of people who make a purchase after hearing an advertisement (a cause-and-effect conclusion). The ideal response also gives the explanation in the context. If a correct explanation is given, but the explanation is not in context, the response is considered to be partially correct.
Responses that indicate that random assignment tends to produce comparable groups or that good experiments include random assignment to treatments but do not specifically tie this to the type of conclusion that can be drawn are also considered to be only partially correct.
Responses that argue only that this is a “fair way” to assign customers to the two experimental groups or that only talk about lack of bias are considered to be incorrect.
Sample responses indicating solid understanding
The following student response shows a good understanding of the concepts assessed by this question and received a score of 4. In part (a), random selection is used to select the sample, and a method is described for how this could be done by numbering the credit card holders from 1 to 5300 and then using a random number generator to select 100 of these customers. The response also indicates that they would make sure that the random numbers generated are different, ensuring that there will be 100 different people in the sample.
The response in part (b) indicates that flipping a coin to determine which advertisement is read results in random assignment to treatments. Had the response stopped there, the response would have been scored as partially correct, but the response goes on to note that this results in being able to conclude cause and effect. The statement about less variability in the results was considered as extraneous and was ignored in the scoring of this part. With both parts scored as essentially correct, this student response received a score of 4.
 In part (a), many students described methods for selection that were equivalent to writing all 5300 names on slips of paper, putting the slips into a hat, and then selecting 100 names. Such responses demonstrated understanding of random selection and were considered to be essentially correct as long as the response indicated that the slips would be mixed before the 100 manes were selected. The response shown below was scored as partially correct, but would have received a score of essentially correct had it included mixing.
In part (a), many students described methods for selection that were equivalent to writing all 5300 names on slips of paper, putting the slips into a hat, and then selecting 100 names. Such responses demonstrated understanding of random selection and were considered to be essentially correct as long as the response indicated that the slips would be mixed before the 100 manes were selected. The response shown below was scored as partially correct, but would have received a score of essentially correct had it included mixing.

Common misunderstandings
Part (a) Recognize the need for random selection and describe a method for selecting a random sample from a given population
Responses that were not scored as essentially correct in part (a) generally made one of two common errors. Some responses indicated random selection, but did not adequately describe a method that could be used to carry out the selection even though the question asked for such a description. The three student responses shown below were scored as partially correct for this reason.


 The other common student error in part (a) was failure to address mixing when trying to describe a method based on drawing names from a hat. The two student responses below were both scored as only partially correct, but would have been scored as essentially correct if they had indicated that the pieces of paper or the cards were mixed before the selection occurred.
The other common student error in part (a) was failure to address mixing when trying to describe a method based on drawing names from a hat. The two student responses below were both scored as only partially correct, but would have been scored as essentially correct if they had indicated that the pieces of paper or the cards were mixed before the selection occurred.


Part (b) Explain why random assignment to treatments is important in the design of a statistical experiment
In part (b), the most common student errors were: (1) failure to link random assignment to the type of conclusion that can be drawn; and (2) giving an explanation based on the fact that the flipping of a coin resulted in a 50-50 chance for each treatment and that this was a fair way to make the decision or a way the eliminated bias.
The two student responses below illustrate this. Both recognize that the method described results in random assignment to treatments, but neither links this to enabling the manager to reach a cause-and-effect conclusion. For this reason, both of these responses were considered to be only partially correct for part (b).

 A number of students indicated that the reason for using the method described to assign card holders to one of the two advertisements was so that the manager would not be able to influence the results. While this is a correct statement, it is not sufficient and fails to recognize the impact on the type of conclusion that can be drawn. This is illustrated in the following two student responses, both of which received a score of partially correct for part (b).
A number of students indicated that the reason for using the method described to assign card holders to one of the two advertisements was so that the manager would not be able to influence the results. While this is a correct statement, it is not sufficient and fails to recognize the impact on the type of conclusion that can be drawn. This is illustrated in the following two student responses, both of which received a score of partially correct for part (b).

 Often student referred only to the fact that the method described is not biased and was a fair way to do the assignment. While these statements are not incorrect, like the responses above they fail to recognize the impact on the type of conclusion that can be drawn. This is illustrated in the following student responses, all of which received a score of partially correct for part (b).
Often student referred only to the fact that the method described is not biased and was a fair way to do the assignment. While these statements are not incorrect, like the responses above they fail to recognize the impact on the type of conclusion that can be drawn. This is illustrated in the following student responses, all of which received a score of partially correct for part (b).



 This question was written to see if students understand the role of random selection and the role of random assignment in statistical studies. While students seemed to have a better understanding of the purpose of and need for random selection when selecting a sample, few students were able to clearly articulate the reason that random assignment is incorporated into the design of statistical experiments.
This question was written to see if students understand the role of random selection and the role of random assignment in statistical studies. While students seemed to have a better understanding of the purpose of and need for random selection when selecting a sample, few students were able to clearly articulate the reason that random assignment is incorporated into the design of statistical experiments.
Student performance
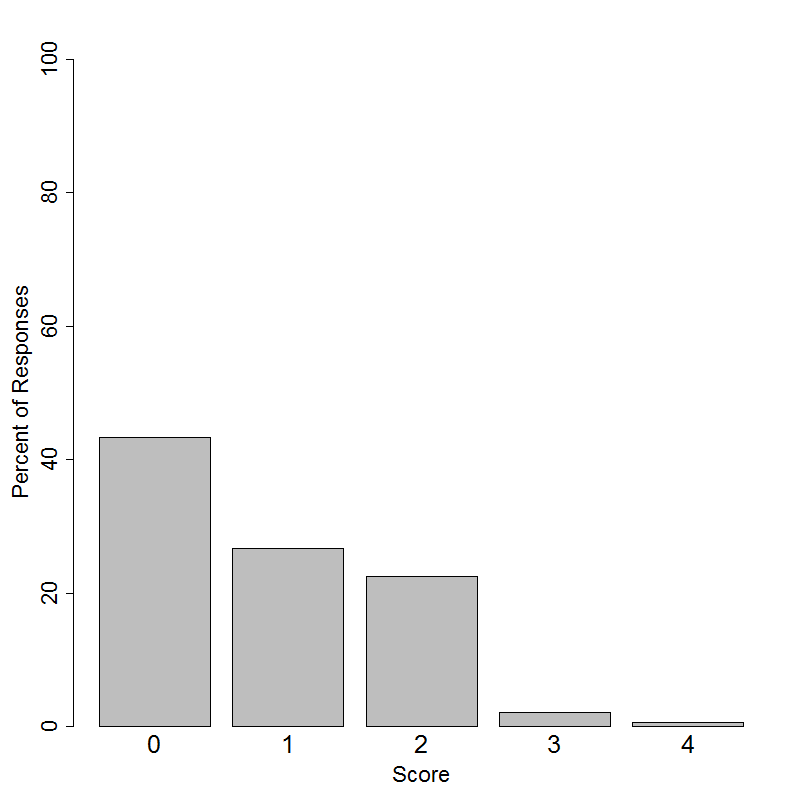
Resources
Free Resources
Webinars
The American Statistical Association has a number of webinars on its web site at
http://www.amstat.org/education/webinars/index.cfm
One webinar related to the topic of this question is the one titled “An Elementary Introduction to Experimental Design”.
Classroom and Assessment Tasks
Illustrative Mathematics has peer reviewed tasks that are indexed by Common Core Standard. A task that focuses on the role of study design in the type of conclusion that can be drawn and could be the basis of a productive classroom discussion is
A task that focuses on the need for random selection in sampling and could be the basis of a productive classroom discussion is
A task that focuses on the need for random assignment is
Guidelines for Assessment and Instruction in Statistics Education (GAISE)
Published by the American Statistical Association and freely available online, this document contains a discussion of the implications of random sampling (pages 52 – 54).
Common Core Progressions Documents
In the Common Core State Standards, random sampling is first introduced in grade 7. A brief discussion of random sampling can be found in the classroom can be found in Common Core Tools progressions document for statistics in grades 6 - 8. See the discussion of random sampling under standard 7.SP.1 on pages 8 – 9.
Resources from the American Statistical Association
Making Sense of Statistical Studies is a collection of investigations suitable for classroom use. The Introduction provides an overview of the statistical problem solving process. A nice discussion of the role of random selection can be found in the introduction to the section on observational studies (pages 10 – 13). A Discussion of the role of random assignment can be found in the introduction to the section on experiments (pages 52 – 66).
Resources from the National Council of Teachers of Mathematics
The NCTM publication Developing Essential Understanding of Statistics in Grades 9 –12 includes a discussion of the importance of the data collection method as Big Idea 4. This resource provides a good discussion of random selection and random assignment, as well as a discussion of how the data collection method affects the types of conclusions that can be drawn from statistical studies (see pages 57 – 66).
The NCTM publication Developing Essential Understanding of Statistics in Grades 6 – 8 includes a discussion of random sampling (see pages 73 – 75) that is relevant to the content assessed in part (a) of this question. For information see



