Stella saw the following headline in a national newspaper: “30 Percent of High School Students Favor Extended School Day.” She wondered if the percentage of students at her school who favor an extended school day was less than 30 percent. To investigate, she selected a random sample of 50 students from the 1,200 students at her school and asked each student in the sample if he or she favors an extended school day.
Only 12 of the students in the sample favored an extended school day. Because the sample percentage is (12/50)100 = 24%, Stella thinks that fewer than 30 percent of the students at her school favor an extended school day. She wonders if it would be surprising to see a sample percentage of 24 or less if the school percentage is
really 30.
(a) To see what values of the sample percentage would be expected if the school percentage was 30, she decides to use 1,200 beads to represent the population of 1,200 students. She will use a red bead to represent a student who favors an extended school day and a white bead to represent a student who does not. How many red beads and how many white beads should Stella use?
Stella put all the beads in a box. After mixing the beads, she selected 50 of them and computed the percentage of red beads. She put the 50 beads back in the box and repeated this process 99 more times. Then, she made the following dotplot of the 100 sample percentages:
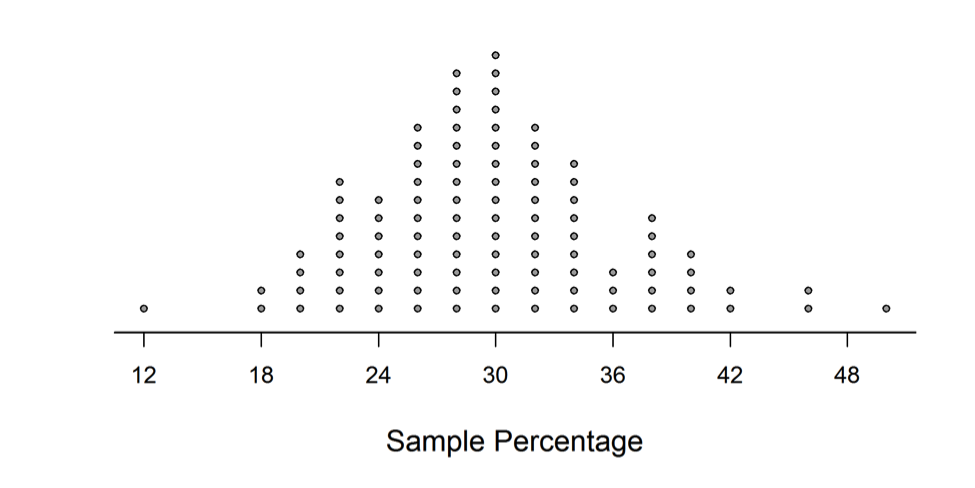 (b) If the school percentage were actually 30%, how surprising would it be to see a sample percentage of 24% or less? Justify your answer using the dotplot.
(b) If the school percentage were actually 30%, how surprising would it be to see a sample percentage of 24% or less? Justify your answer using the dotplot.
(c) Based on her sample data, should Stella conclude that the percentage of students at the school who favor an extended school day is less than 30%? Explain why or why not.





 The following student response also received a score of 4, and illustrates the need to read parts (b) and (c) together. Part (c) by itself is not complete, but the necessary explanation is given in part (b).
The following student response also received a score of 4, and illustrates the need to read parts (b) and (c) together. Part (c) by itself is not complete, but the necessary explanation is given in part (b).
 There are a number of ways that a student could demonstrate understanding of the concepts assessed in parts (b) and (c). For example, the following responses were also scored as essentially correct for both parts (b) and (c) (read and scored together):
There are a number of ways that a student could demonstrate understanding of the concepts assessed in parts (b) and (c). For example, the following responses were also scored as essentially correct for both parts (b) and (c) (read and scored together):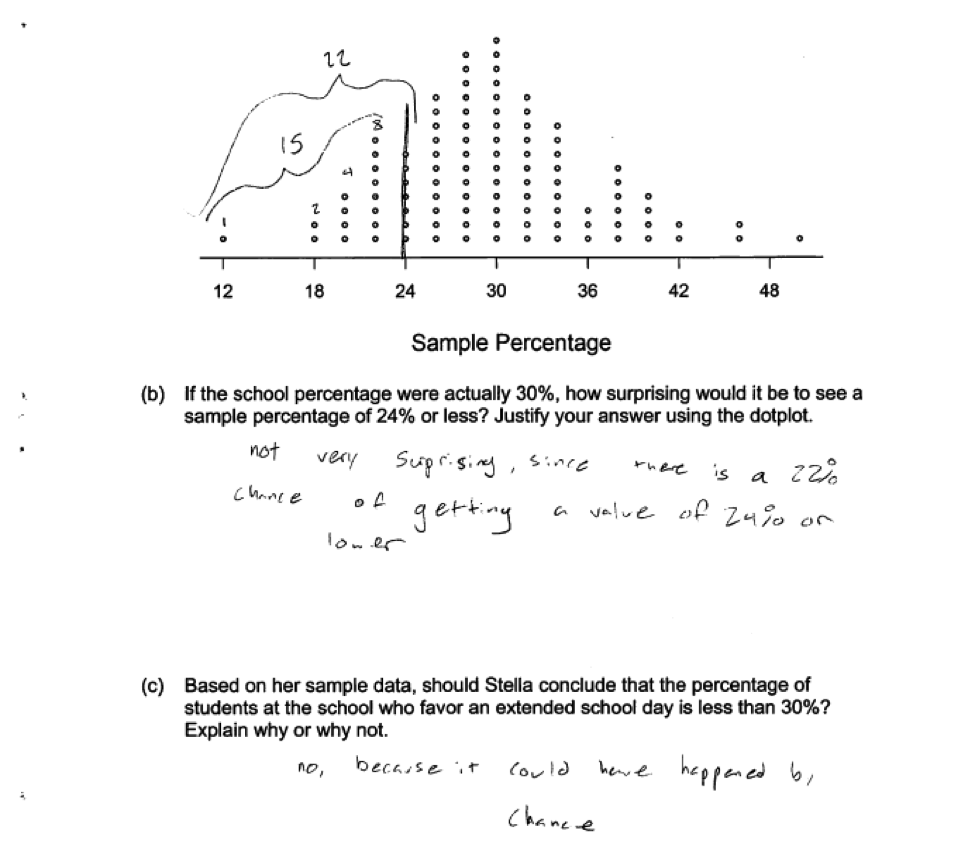

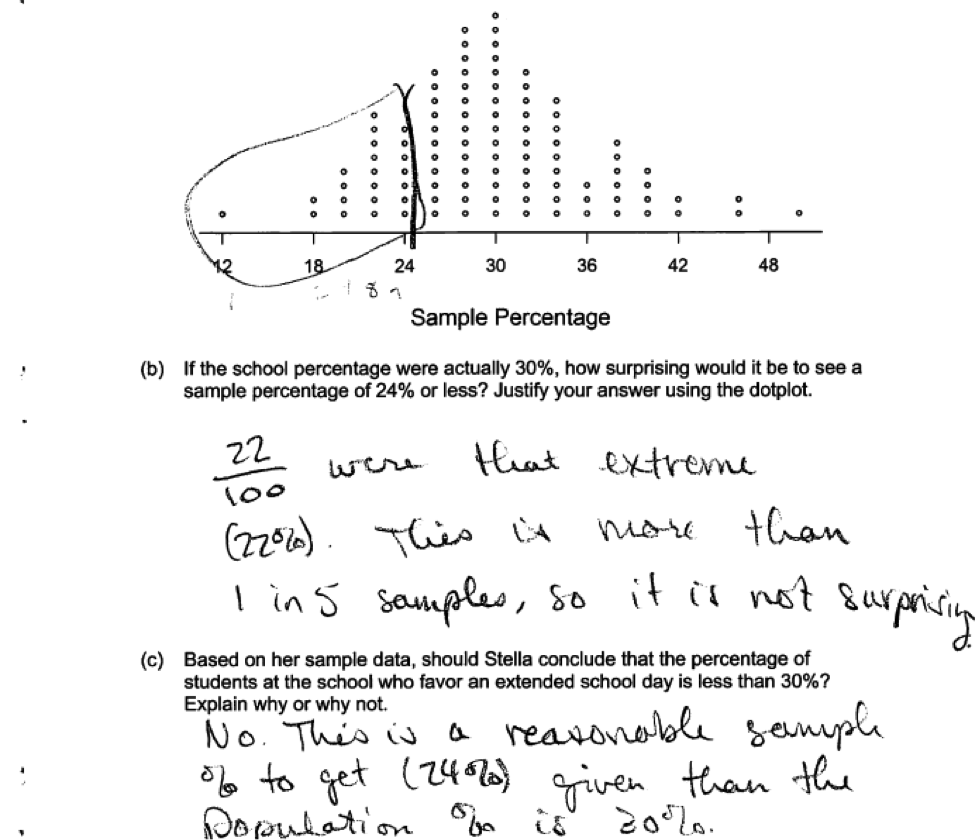 The following response was scored as partially correct for part (b) because the explanation does not provide a clear link to the given simulated sampling distribution. The question specifically asks for an explanation in terms of the dotplot.
The following response was scored as partially correct for part (b) because the explanation does not provide a clear link to the given simulated sampling distribution. The question specifically asks for an explanation in terms of the dotplot. Another example of a response to part (b) that shows understanding of the underlying concepts but which was considered only partially correct is shown below. In this response, the p-value is computed incorrectly.
Another example of a response to part (b) that shows understanding of the underlying concepts but which was considered only partially correct is shown below. In this response, the p-value is computed incorrectly.


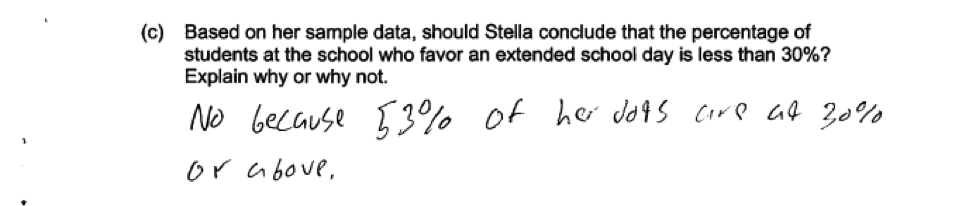 Another student error resulting from failure to understand the simulated sampling distribution is illustrated in the following response. In this response, it is clear that the student does not understand that the dots in the dotplot represent a percentage based on a sample of 50 students from a population in which 30% of the students favor an extended school day and that the student is interpreting the dots in the dotpot as somehow representing individual students.
Another student error resulting from failure to understand the simulated sampling distribution is illustrated in the following response. In this response, it is clear that the student does not understand that the dots in the dotplot represent a percentage based on a sample of 50 students from a population in which 30% of the students favor an extended school day and that the student is interpreting the dots in the dotpot as somehow representing individual students. Some student responses demonstrated that the student did not really understand the concept of sampling variability, indicating that it would be reasonable to conclude that the population percentage was less than 30% because most of the dots in the dotplot of the simulated sampling distribution represented values that were 30 or less. This is illustrated in the following responses.
Some student responses demonstrated that the student did not really understand the concept of sampling variability, indicating that it would be reasonable to conclude that the population percentage was less than 30% because most of the dots in the dotplot of the simulated sampling distribution represented values that were 30 or less. This is illustrated in the following responses.
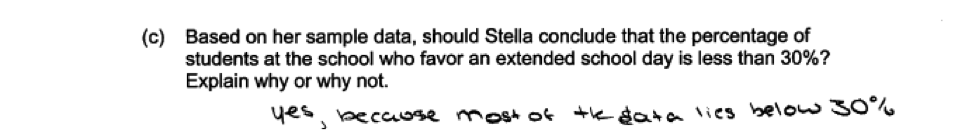 Another common mistake was to focus on the sample size. Even thought the sample size was 50, many responses indicated that no conclusion could be drawn because the sample size was too small. This is illustrated in the following responses.
Another common mistake was to focus on the sample size. Even thought the sample size was 50, many responses indicated that no conclusion could be drawn because the sample size was too small. This is illustrated in the following responses.
 Finally, some students did not understand the purpose of simulation in this context, as illustrated in the following response.
Finally, some students did not understand the purpose of simulation in this context, as illustrated in the following response.