The dotplots below show the distribution of the number of pockets on clothing for a group of 12 boys and for a group of 13 girls.
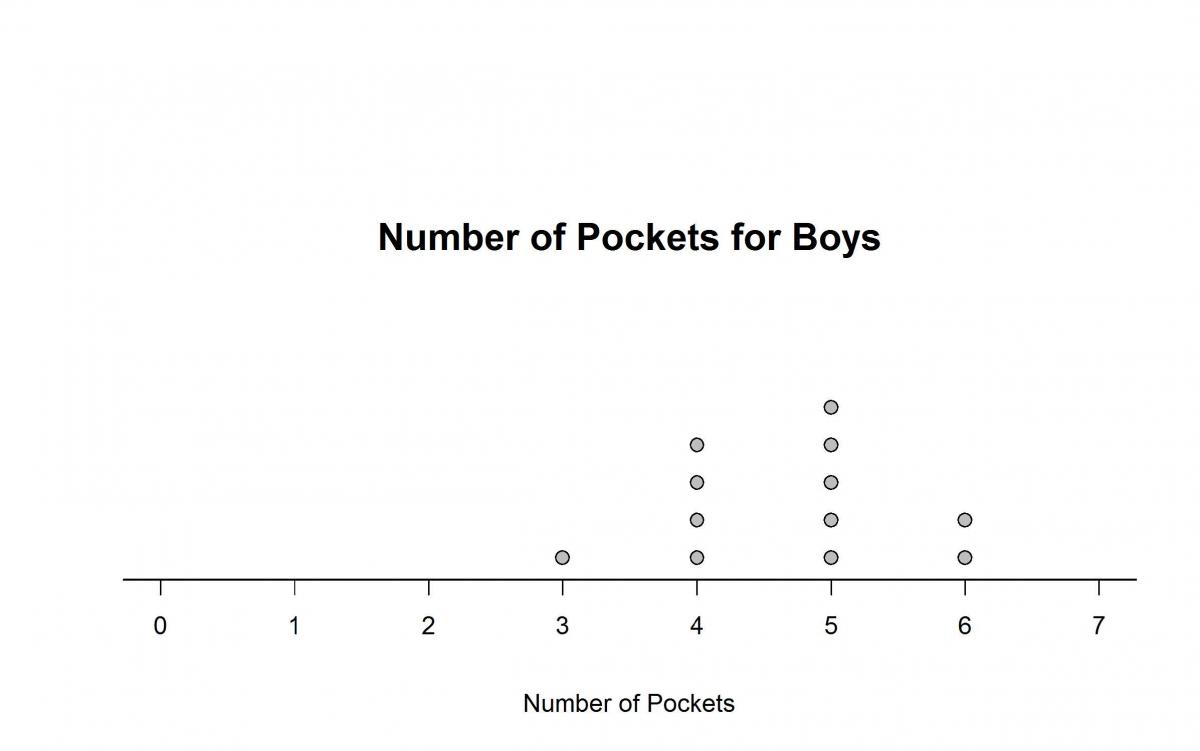
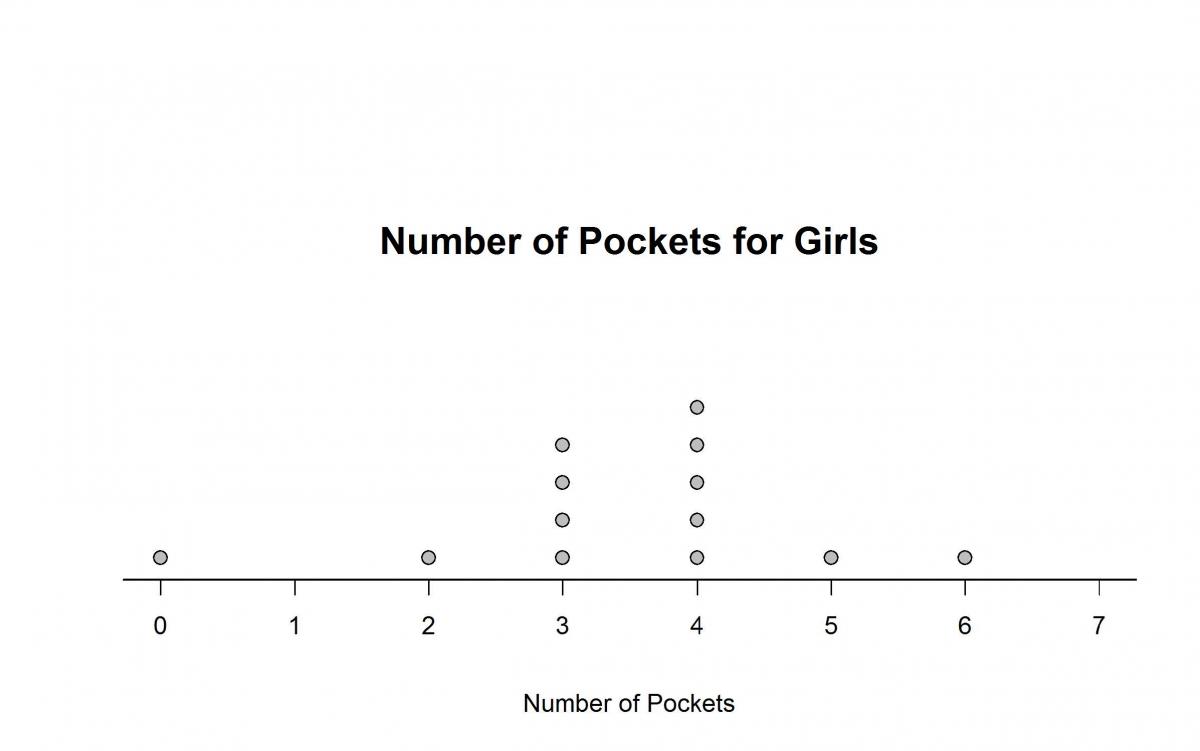
Based on the graphs, which of the following statements is true?
(A) The data vary more for the boys than for the girls.
(B) The median number of pockets for boys is larger than the median for girls.
(C) The mode for the boys and for the girls is 4.
(D) The maximum number of pockets for boys is larger than the maximum number of pockets for girls.




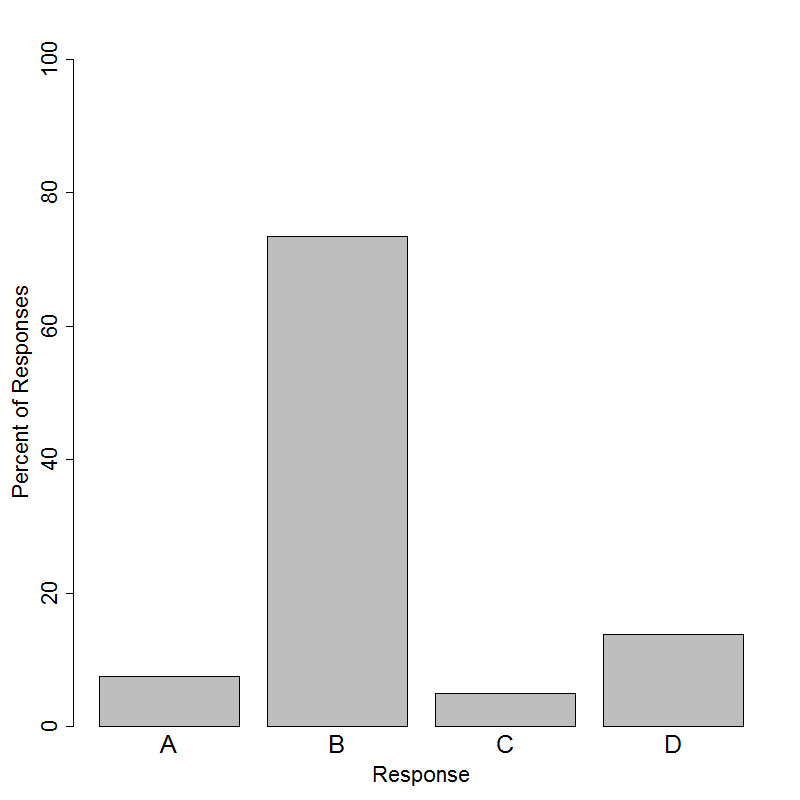
The correct answer to this question is Option (B). The question requires students to use dotplots to find and compare the medians of two distributions. For boys, the average of the two middle values in the data set is 5; for girls, the middle value in the data set is 4. The median number of pockets is larger for boys than for girls, which suggests that the “typical” boy in this sample has more pockets than the “typical” girl.
Beginning in grade 6, students are expected to go beyond calculating measures of center such as the mean and median to considering other features of a distribution including shape and spread. Option (A) refers to the spread of these two distributions. Whether students calculate a numerical measure of spread such as the range, interquartile range (IQR), or mean absolute deviation (MAD), or they just visually assess the distributions, they should conclude that the data vary more for girls than for boys, so Option (A) is incorrect.
Options (C) and (D) refer to two other numerical summaries of data. The mode – the most frequently occurring number of pockets – is 4 for girls, but it is 5 for boys, so Option (C) is incorrect. The maximum number of pockets is 6 for both boys and girls, so Option (D) is incorrect. This answer choice may be tempting for some students, because there are two boys with 6 pockets and only one girl with 6 pockets, making the stack of dots at the maximum larger for boys than for girls.